Pythonで時系列分析（飛行機乗客数）

Matplotlib Python Python時系列分析 データ解析

Pythonで時系列分析（飛行機乗客数）

Pythonで簡単な時系列分析を行う方法です。分析データはRの組み込みデータとして有名なAirPassengers（飛行機乗客数）を利用します。時系列データのグラフ化や成分分離（トレンド、季節、残渣）、モデルによる未来予測など、コード実装を主に記載しています。


PandasとStatsModelsを使って飛行機乗客数の時系列分析を行う


時系列分析（Python）

jupyter notebookを利用し、以下の手順で記載しています。

  • ライブラリーのインポートとグラフ描画準備 ...[1,2]
  • Pandasで分析用データの読み込み（CSVファイルを利用） ...[3,4]
  • 乗客数の時系列データをグラフで確認 ...[5]
  • トレンド、季節、残差成分に分離してデータを可視化 ...[6]
  • 対数変換したデータもグラフで確認 ...[7]
  • 自己相関(acf)と偏自己相関(pacf)をグラフで確認 ...[8]
  • SARIMAモデルの作成（季節自己回帰和分移動平均） ...[9]
  • モデルを使って未来データを予測、グラフ化 ...[10-12]

In [1]:
# ライブラリーインポート、グラフ描画準備
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm
% matplotlib inline
plt.style.use('ggplot')
plt.xkcd()
Out[1]:
<matplotlib.rc_context at 0xad5ba88c>
In [2]:
# statsmodelsのバージョン確認
sm.version.full_version # SARIMAX利用に0.8.0以上が必要
Out[2]:
'0.8.0'
In [3]:
# PandasでCSVファイルを読み込む
# 『AirPassengers.csv』は以下の外部サイトよりダウンロードしたファイルを利用
# https://www.analyticsvidhya.com/wp-content/uploads/2016/02/AirPassengers.csv

df = pd.read_csv('AirPassengers.csv',
                 index_col=0, parse_dates=[0], dtype='float')

print(len(df)) # 144データ（1949年1月から1960年12月まで、月毎の飛行機乗客数）
df.head()

144
Out[3]:
#Passengers
Month
1949-01-01 112.0
1949-02-01 118.0
1949-03-01 132.0
1949-04-01 129.0
1949-05-01 121.0
In [4]:
# pandasのSeriesに乗客数データを格納
ts = df['#Passengers']
In [5]:
# 乗客数データをグラフで可視化(pandas.plot)
ts.plot(figsize=(8, 2))
Out[5]:
<matplotlib.axes._subplots.AxesSubplot at 0xab7bc58c>
In [6]:
# オリジナル ->トレンド成分、季節成分、残差成分に分解してプロット
res = sm.tsa.seasonal_decompose(ts)

trend = res.trend
seasonal = res.seasonal
residual = res.resid

plt.figure(figsize=(8, 8))

# オリジナルの時系列データプロット
plt.subplot(411)
plt.plot(ts)
plt.ylabel('Original')

# trend のプロット
plt.subplot(412)
plt.plot(trend)
plt.ylabel('Trend')

# seasonal のプロット
plt.subplot(413)
plt.plot(seasonal)
plt.ylabel('Seasonality')

# residual のプロット
plt.subplot(414)
plt.plot(residual)
plt.ylabel('Residuals')

plt.tight_layout()
In [7]:
# log変換データで確認
ts_log = np.log(ts)
res_log = sm.tsa.seasonal_decompose(ts_log)
trend_log = res_log.trend
seasonal_log = res_log.seasonal
residual_log = res_log.resid
plt.figure(figsize=(8, 8))
# オリジナルlog変換
plt.subplot(411)
plt.plot(ts_log, c='b')
plt.ylabel('Original')
# trend
plt.subplot(412)
plt.plot(trend_log, c='b')
plt.ylabel('Trend')
# seasonal
plt.subplot(413)
plt.plot(seasonal_log, c='b')
plt.ylabel('Seasonality')
# residual
plt.subplot(414)
plt.plot(residual_log, c='b')
plt.ylabel('Residuals')
plt.tight_layout()
In [8]:
# 自己相関(acf)のグラフ
fig = plt.figure(figsize=(8, 8))
ax1 = fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(ts, lags=48, ax=ax1)
# 偏自己相関(pacf)のグラフ
ax2 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(ts, lags=48, ax=ax2)
plt.tight_layout()
In [9]:
# SARIMAモデル（季節自己回帰和分移動平均モデル）
#import warnings
#warnings.filterwarnings('ignore') # warnings非表示
srimax = sm.tsa.SARIMAX(ts, order=(2,1,3),
                            seasonal_order=(0,2,2,12),
                            enforce_stationarity = False,
                            enforce_invertibility = False
                           ).fit()
# order=(2,1,3), season=(0,2,2)  -> aic 705.953
# print(srimax.summary())
# Warnings:
# [1] Covariance matrix calculated using the outer product of gradients (complex-step).
In [10]:
# 未来データ予測
pred = srimax.forecast(24) # 未来の24データ予測
pred[:10]
Out[10]:
1961-01-01    457.165805
1961-02-01    416.156322
1961-03-01    470.170182
1961-04-01    494.344642
1961-05-01    500.944028
1961-06-01    578.199221
1961-07-01    668.960965
1961-08-01    654.405477
1961-09-01    552.007646
1961-10-01    498.787664
Freq: MS, dtype: float64
In [11]:
# 未来データ予測
pred = srimax.forecast(24) # 未来の24データ予測

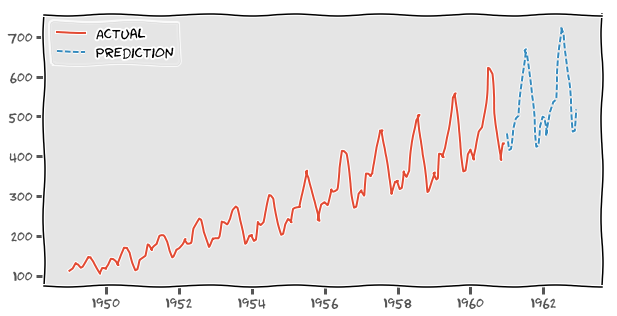
# 実データと予測データのグラフ描画
plt.figure(figsize=(10, 5))
plt.plot(ts, label='Actual')
plt.plot(pred, label='Prediction', linestyle='--')
plt.legend(loc='best')
Out[11]:
<matplotlib.legend.Legend at 0xaa0ab22c>
In [12]:
# データ予測（期間指定）
predict_fromTo = srimax.predict('1954-01-01', '1962-12-01')

# 実データと予測データのグラフ描画
plt.figure(figsize=(10, 5))
plt.plot(ts, label='Actual')
plt.plot(predict_fromTo, label='Prediction', alpha=0.5)
plt.legend(loc='best')
Out[12]:
<matplotlib.legend.Legend at 0xaa1771ac>


詳細は以下の記事にも記載しています。



スポンサーリンク

0 件のコメント :

コメントを投稿