パーセプトロン
パーセプトロンとは、脳などの神経細胞(ニューロン)の機能をモデル化したものです。複数の信号を入力として受けとり、単一の信号を出力します。出力信号は、入力の総和がある一定の値(閾値)を超えると出力され、発火とも表現されます(2値の場合は1を出力)。パーセプトロンを多層化したニューラルネットワーク(多層パーセプトロン)は、Deep Learningの要素技術して使われています。
パーセプトロン、Pythonコードで論理回路を作る
AND回路とOR回路、NAND回路は、単一のパーセプトロンで実現できます。信号を0と1の2値とすると、入出と出力の対応は以下のように表現できます。AND回路(アンド)
入力x1および入力x2が共に1のときだけ1を出力。それ以外の入力では0を出力します。| 入力x1 | 入力x2 | 出力 |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
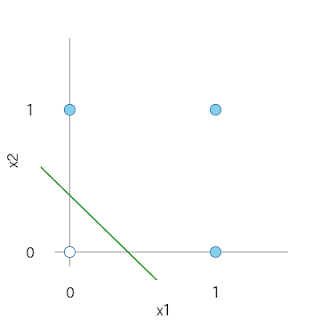
グラフで表現すると、出力値はグリーンのような直線で区切ることができます。
白抜きの青〇は出力0、塗りつぶした青●が出力1に対応します。
なお、グラフ上のグリーン線は一例です。適応可能な切片や傾きの異なる直線は無限に存在します。
【グラフ】
パーセプトロンは、以下の形式図や数式で表現することができます。
【形式図】パーセプトロン(2入力)
図でx1,x2が入力値、w1,w2は入力値に乗算する重み定数、Θは閾値の定数です。入力xと重みwの積和が閾値Θを超える、超えないかで出力が決まります。出力が2値の場合は閾値Θを超えたときに1を出力します(発火)。
出力値は、定数の重みwと閾値Θに適正なパラメータ値を選ぶことで目的とする結果が得られます。機会学習は最適なパラメータを求めるためデータをもとに学習を行います。
【数式】
入力値x1x2、重みw1w2、閾値Θとすると、2値の出力値は以下の式で場合分けできます。 \begin{eqnarray} output = \begin{cases} 0 & ( w_1x_1 + w_2x_2 \geq \theta ) \\ 1 & ( w_1x_1 + w_2x_2 \lt \theta ) \end{cases} \end{eqnarray}
また、Θは一般的に、-bとも表現されるため以下ように書き換えできます。 \begin{eqnarray} output = \begin{cases} 0 & ( w_1x_1 + w_2x_2 \geq -b ) \\ 1 & ( w_1x_1 + w_2x_2 \lt -b ) \end{cases} \end{eqnarray}
さらに、-bを左辺に移行するとよく見かける式に変形できます。 \begin{eqnarray} output = \begin{cases} 0 & ( b + w_1x_1 + w_2x_2 \geq 0 ) \\ 1 & ( b + w_1x_1 + w_2x_2 \lt 0 ) \end{cases} \end{eqnarray}
bはバイアスと呼ばれています。
左辺0のときがグリーンの直線上です。 \[b + w_1x_1 + w_2x_2 = 0\] 一般的な直線の方程式 y = ax + bの形にすると、 \[x_2 = - \frac{w_1}{w_2}x_1 - \frac{b}{w_2}\]
上のグラフでは重みW1,W2をそれぞれ0.5、バイアスbを-0.7に設定しています。
よってグラフ上で緑の直線の式は以下となります。 \[x_2 = - \frac{0.5}{0.5}x_1 - \frac{(-0.7)}{0.5}\] \[x_2 = - x_1 + 1.4\]
PythonでAND回路を簡易実装した例です。
def AND(x1, x2):
w1, w2, b = [0.5, 0.5, -0.7]
tmp = w1 * x1 + w2 * x2 + b
return 0 if tmp <=0 else 1
print("AND(0, 0) -> " , AND(0, 0)) # 0
print("AND(0, 1) -> " , AND(1, 0)) # 0
print("AND(1, 0) -> " , AND(0, 1)) # 0
print("AND(1, 1) -> " , AND(1, 1)) # 1
OR回路(オア)
入力x1または入力x2が1ときに1を出力。入力x1とx2が共に0のときだけ0を出力します。| 入力x1 | 入力x2 | 出力 |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
グラフのグリーン線をANDのときよりも下方にシフトすると、OR出力ができます。
OR回路のPythonコード実装例です。
In [1]:
def OR(x1, x2):
w1, w2, b = [0.5, 0.5, -0.2]
tmp = w1 * x1 + w2 * x2 + b
return 0 if tmp <=0 else 1
print("OR(0, 0) -> " , OR(0, 0)) # 0
print("OR(0, 1) -> " , OR(1, 0)) # 1
print("OR(1, 0) -> " , OR(0, 1)) # 1
print("OR(1, 1) -> " , OR(1, 1)) # 1
NAND回路(ナンド)
Not ANDの略語。入力x1および入力x2がともに1ときだけ0を出力します。(ANDの反転出力)| 入力x1 | 入力x2 | 出力 |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
NANDは符号を反転すると同じような表現ができます。
NAND回路のPythonコード実装例です。
def NAND(x1, x2):
w1, w2, b = [-0.5, -0.5, 0.7]
tmp = w1 * x1 + w2 * x2 + b
return 0 if tmp <=0 else 1
print("NAND(0, 0) -> " , NAND(0, 0)) # 1
print("NAND(0, 1) -> " , NAND(1, 0)) # 1
print("NAND(1, 0) -> " , NAND(0, 1)) # 1
print("NAND(1, 1) -> " , NAND(1, 1)) # 0
XOR回路(エクスクルーシブ・オア)
入力x1と入力x2が異なるときに1を出力(一方が1で他方は0)。入力x1と入力x2が同じときは0を出力します。| 入力x1 | 入力x2 | 出力 |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
グラフでプロットの配置からも分かるように、XORの出力は1本の直線では区切ることができません(つまり単一のパーセプトロンでは実現不可)。
XORは複数のパーセプトロンを多層にすることで実現できます。具体的にはNAND、OR、ANDの三つを組み合わせることで目的の出力値が得られます。
組み合わせた方は、まず、NANDとORそれぞれに入力値を与える。NAND、ORそれぞれの出力値をさらにANDの入力値として渡す。その結果でXORを得ることができます。
XORを表計算ソフトの関数風に書くと以下のようになります。
= AND(NAND(入力x1, 入力x2), OR(入力x1, 入力x2))
XOR回路のPythonコード実装例です。
def AND(x1, x2):
w1, w2, b = [0.5, 0.5, -0.7]
tmp = w1 * x1 + w2 * x2 + b
return 0 if tmp <=0 else 1
def OR(x1, x2):
w1, w2, b = [0.5, 0.5, -0.2]
tmp = w1 * x1 + w2 * x2 + b
return 0 if tmp <=0 else 1
def NAND(x1, x2):
w1, w2, b = [-0.5, -0.5, 0.7]
tmp = w1 * x1 + w2 * x2 + b
return 0 if tmp <=0 else 1
def XOR(x1, x2):
tmp1 = NAND(x1, x2)
tmp2 = OR(x1, x2)
return AND(tmp1, tmp2)
print("XOR(0, 0) -> " , XOR(0, 0)) # 0
print("XOR(0, 1) -> " , XOR(1, 0)) # 1
print("XOR(1, 0) -> " , XOR(0, 1)) # 1
print("XOR(1, 1) -> " , XOR(1, 1)) # 0
参考まで、論理回路のグラフとPythonコードはJupyter Notebook、パーセプトロン形式図はエクセルで作成しています。








0 件のコメント :
コメントを投稿